The paper “Distributional robustness in minimax linear quadratic control with Wasserstein distance” has been published in the SIAM Journal on Control and Optimization.

Distributional robustness in minimax linear quadratic control with Wasserstein distance
by Kihyun Kim, and Insoon Yang

Abstract:
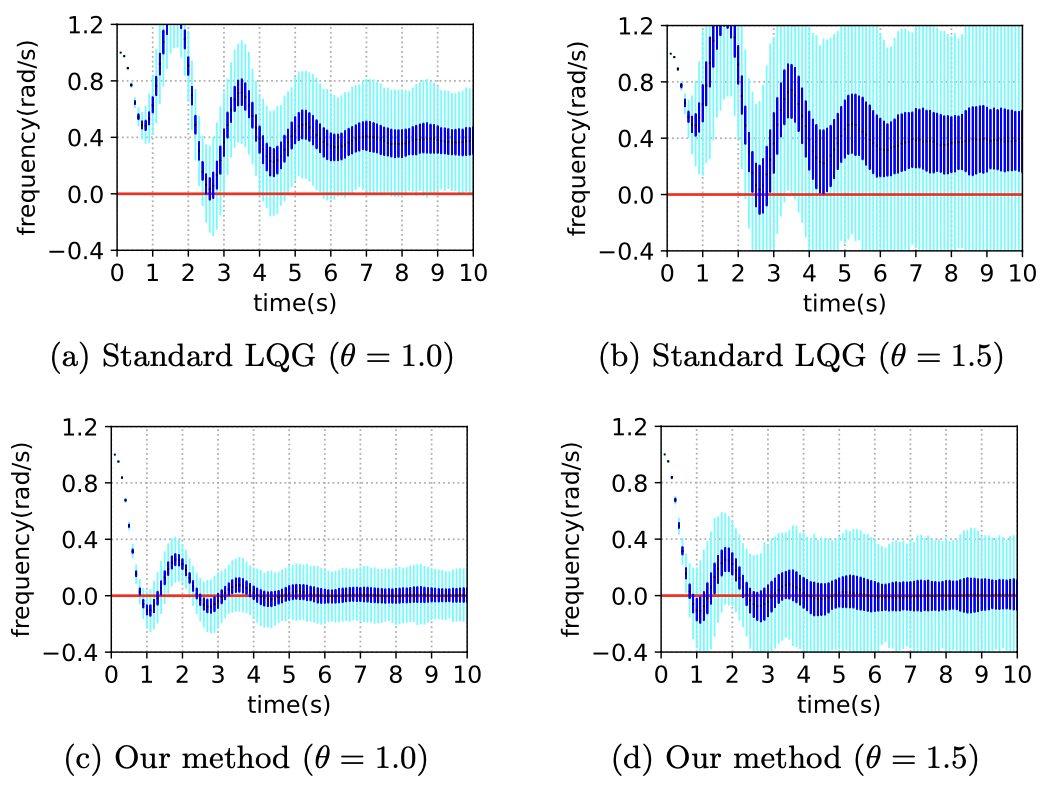
To address the issue of inaccurate distributions in discrete-time stochastic systems, a minimax linear quadratic control method using the Wasserstein metric is proposed. Our method aims to construct a control policy that is robust against errors in an empirical distribution of underlying uncertainty by adopting an adversary that selects the worst-case distribution at each time. The opponent receives a Wasserstein penalty proportional to the amount of deviation from the empirical distribution. As a tractable solution, a closed-form expression of the optimal policy pair is derived using a Riccati equation. We identify nontrivial stabilizability and observability conditions under which the Riccati recursion converges to the unique positive semidefinite solution of an algebraic Riccati equation. Our method is shown to possess several salient features, including closed-loop stability, a guaranteed-cost property, and a probabilistic out-of-sample performance guarantee.