![[CDC (2 papers)] Anderson acceleration for POMDPs, Distributionally robust control in learning-enabled environments](http://coregroup.snu.ac.kr/wp-content/uploads/2018/11/Depositphotos_4892867_xl-2015.jpg)
The papers “On Anderson Acceleration for Partially Observable Markov Decision Processes”, and “Improving the Distributional Robustness of Risk-Aware Controllers in Learning-Enabled Environments” have been accepted to the IEEE Conference on Decision and Control (CDC).
On Anderson Acceleration for Partially Observable Markov Decision Processes
by Melike Ermis, Mingyu Park, and Insoon Yang
Abstract: This paper proposes an accelerated method for approximately solving partially observable Markov decision process (POMDP) problems offline. Our method carefully combines two existing tools: Anderson acceleration (AA) and the fast informed bound (FIB) method. Adopting AA, our method rapidly solves an approximate Bellman equation with an efficient combination of previous solution estimates. Furthermore, the use of FIB alleviates the scalability issue inherent in POMDPs. We show the convergence of the overall algorithm to the suboptimal solution obtained by FIB. We further consider a simulation-based method and prove that the approximation error is bounded explicitly. The performance of our algorithm is evaluated on several benchmark problems. The results of our experiments demonstrate that the proposed algorithm converges significantly faster without degrading the quality of the solution compared to its standard counterpart.
Improving the Distributional Robustness of Risk-Aware Controllers in Learning-Enabled Environments
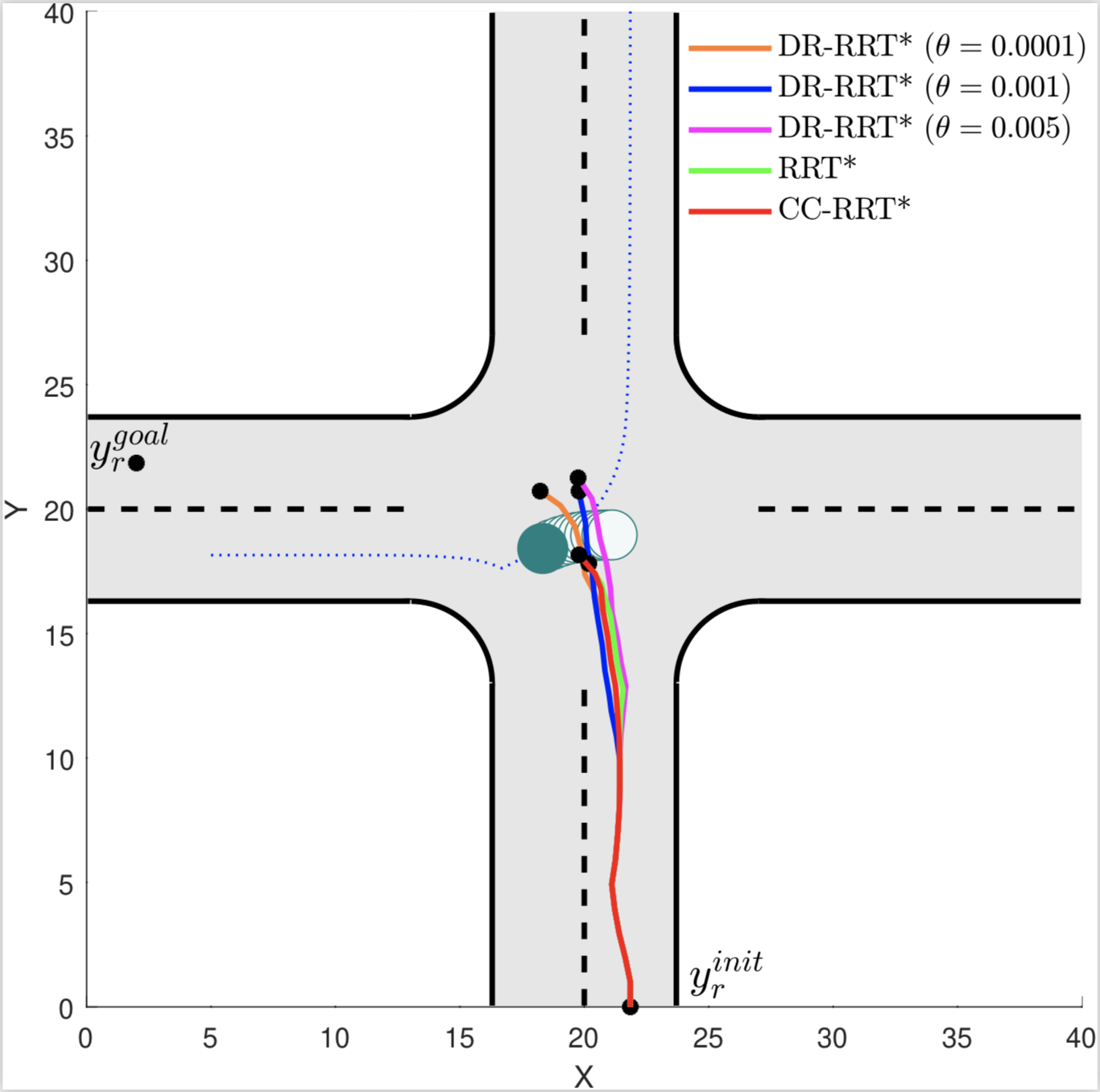
by Astghik Hakobyan, and Insoon Yang
Abstract: This paper concerns with designing a risk-aware controller in an unknown and dynamic environment. In our method, the evolution of the environment state is learned using observational data via Gaussian process regression (GPR). Un- fortunately, the learning result provides imperfect distribution information about the environment. To address such distribution errors, we propose a risk-constrained model predictive control (MPC) method exploiting tools from distributionally robust optimization (DRO). To resolve the infinite dimensionality issue inherent in DRO, we derive a tractable semidefinite programming (SDP) problem that upper-bounds the original MPC problem. Furthermore, the SDP problem is reduced to a quadratic program when the constraint function has a decomposable form. As another salient feature, our controller is shown to provide a performance guarantee on the true risk value in the presence of the prediction errors caused by GPR. The performance and utility of our method are demonstrated through simulations on an autonomous driving problem, showing that our controller preserves safety despite errors in learning the behaviors of surrounding vehicles.
