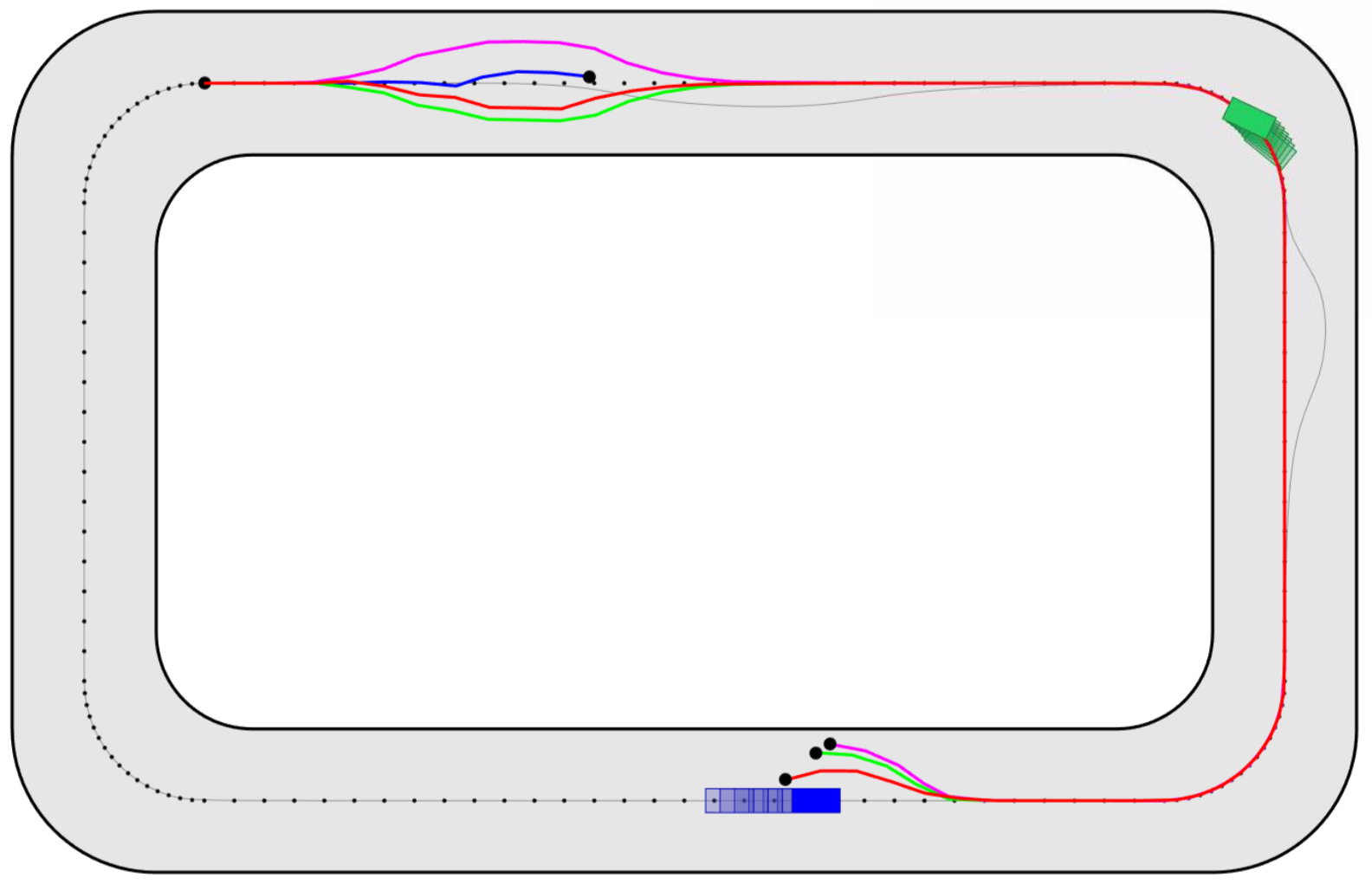
The paper “Learning-based distributionally robust motion control with Gaussian processes“, authored by Astghik Hakobyan, and Insoon Yang, has been accepted to the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). This paper emphasizes the importance of “control” in correcting potential errors in “learning”. The key idea is to determine the motion control action that is robust against errors in learned information about the obstacles’ motion. Specifically, our method uses Gaussian process (GP) regression to estimate the probability distribution of the obstacles’ locations for future stages based on the current and past observations. To actively take into account the possibility that the learned distribution information may be inaccurate, we propose a novel MPC method that optimizes the motion control action subject to constraints on the risk of unsafety evaluated under the worst-case distribution in a so-called ambiguity set. Thus, the resulting control action will satisfy the risk constraints for safety even when the true distribution deviates from the learned one within the ambiguity set.

Youtube: https://www.youtube.com/watch?v=3PLCw4vqfQ0

Abstract: Safety is a critical issue in learning-based robotic and autonomous systems as learned information about their environments is often unreliable and inaccurate. In this paper, we propose a risk-aware motion control tool that is robust against errors in learned distributional information about obstacles moving with unknown dynamics. The salient feature of our model predictive control (MPC) method is its capability of limiting the risk of unsafety even when the true distribution deviates from the distribution estimated by Gaussian process (GP) regression, within an ambiguity set. Unfortunately, the distributionally robust MPC problem with GP is intractable because the worst-case risk constraint involves an infinite-dimensional optimization problem over the ambiguity set. To remove the infinite-dimensionality issue, we develop a systematic reformulation approach exploiting modern distributionally robust optimization techniques. The performance and utility of our method are demonstrated through simulations using a nonlinear car-like vehicle model for autonomous driving.