The paper “Hamilton-Jacobi-Bellman equations for Q-learning in continuous time“, authored by Jeongho Kim, and Insoon Yang, has been accepted to the Conference on Learning for Dynamics and Control (L4DC). This paper introduces a novel class of Hamilton-Jacobi-Bellman (HJB) equations that allow us to perform Q-learning for continuous-time dynamical systems in a principled way.
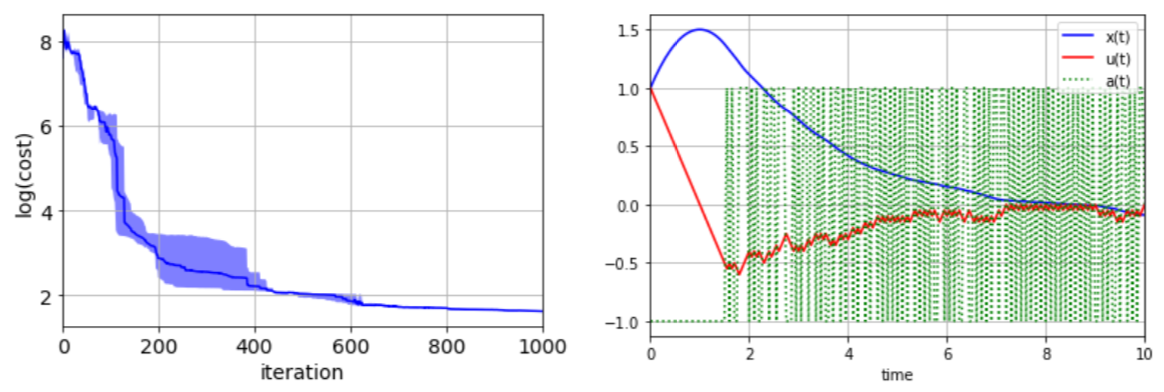
Abstract: In this paper, we introduce Hamilton-Jacobi-Bellman (HJB) equations for Q-functions in continuous time optimal control problems with Lipschitz continuous controls. The standard Q-function used in reinforcement learning is shown to be the unique viscosity solution of the HJB equation. A necessary and sufficient condition for optimality is provided using the viscosity solution framework. By using the HJB equation, we develop a Q-learning method for continuous-time dynamical systems. A DQN-like algorithm is also proposed for high-dimensional state and control spaces. The performance of the proposed Q-learning algorithm is demonstrated using 1-, 10- and 20-dimensional dynamical systems.





